Associativity: If an expression contains two or more operators with the same precedence then Operator Associativity is used to determine. It can either be Left to Right or from Right to Left.
| Operator | Description | Associativity |
|---|---|---|
| ( ) | Parentheses | left-to-right |
| ** | Exponent | right-to-left |
| * / % | Multiplication/division/modulus | left-to-right |
| + – | Addition/subtraction | left-to-right |
| << >> | Bitwise shift left, Bitwise shift right | left-to-right |
| < <= > >= | Relational less than/less than or equal to Relational greater than/greater than or equal to | left-to-right |
| == != | Relational is equal to/is not equal to | left-to-right |
is, is not in, not in | Identity Membership operators | left-to-right |
| & | Bitwise AND | left-to-right |
| ^ | Bitwise exclusive OR | left-to-right |
| | | Bitwise inclusive OR | left-to-right |
| not | Logical NOT | right-to-left |
| and | Logical AND | left-to-right |
| or | Logical OR | left-to-right |
| = += -= *= /= %= &= ^= |= <<= >>= | Assignment Addition/subtraction assignment Multiplication/division assignment Modulus/bitwise AND assignment Bitwise exclusive/inclusive OR assignment Bitwise shift left/right assignment |
Example: ‘*’ and ‘/’ have the same precedence and their associativity is Left to Right, so the expression “100 / 10 * 10” is treated as “(100 / 10) * 10”.
Code:
- Python3
Output:
100 6 0 512
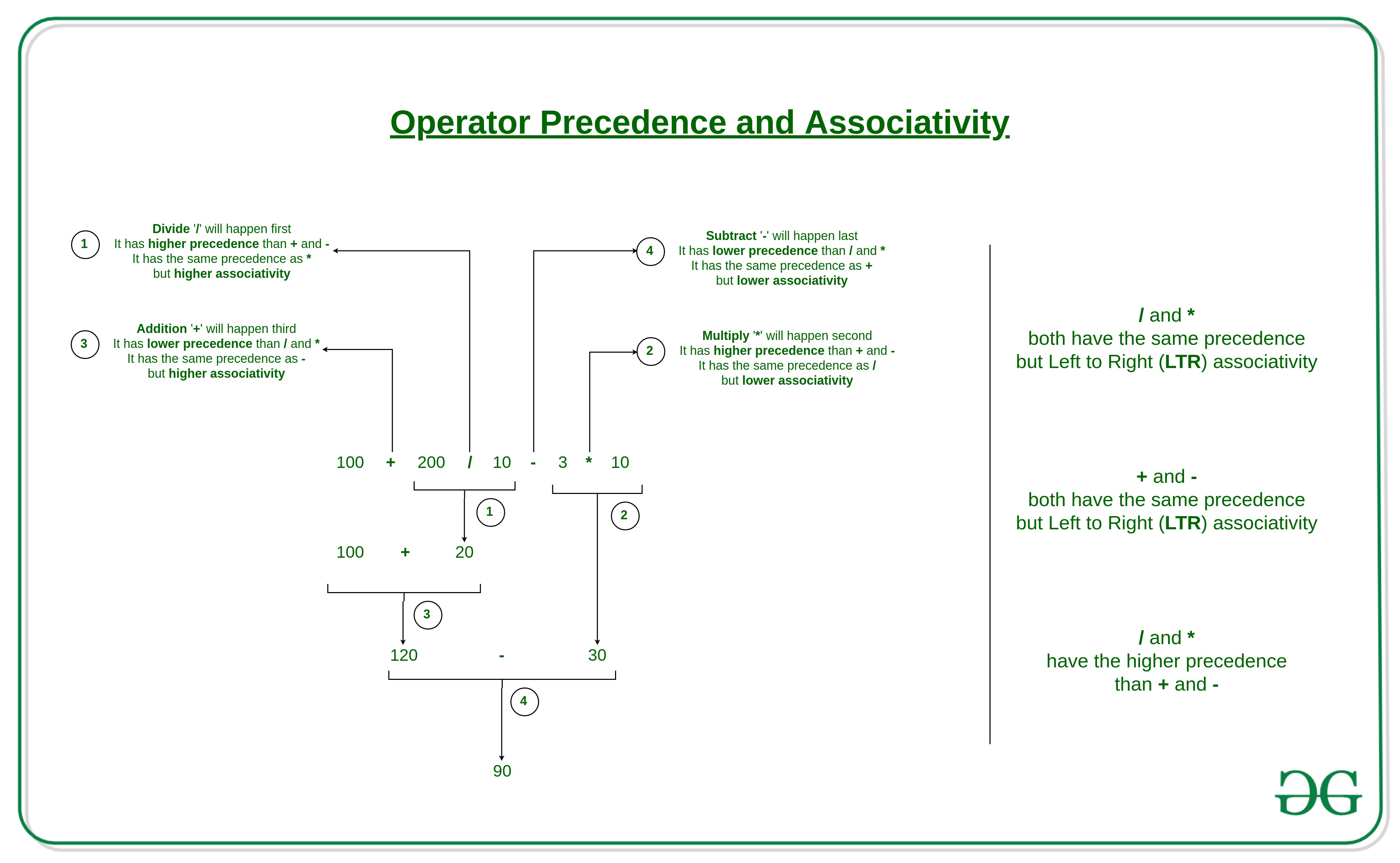
Operators Precedence and Associativity are two main characteristics of operators that determine the evaluation order of sub-expressions in absence of brackets.
Example: Solve
100 + 200 / 10 - 3 * 10
100 + 200 / 10 - 3 * 10 is calculated as 100 + (200 / 10) - (3 * 10) and not as (100 + 200) / (10 - 3) * 10
Code:
- Python3
Output:
90.0